图论基础

图的概念

图论是离散数学的一个分支，致力于研究图（Graph）这一数学结构。图是用来模拟对象之间成对关系的工具，由节点或顶点（Vertex）以及连接这些顶点的边（Edge）组成。

下面这张图片就是一个图$G(V,E)$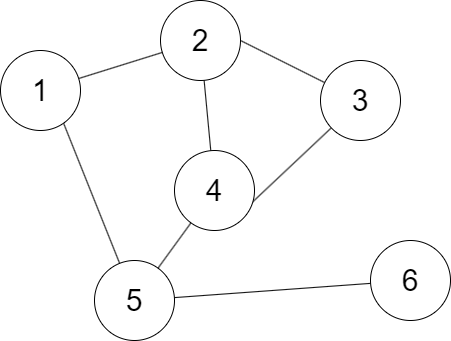

图可以被表示为 $G=(V, E)，其中 V=(v_1, … , v_N)，E= (e_1, … , e_M)$。

其中$V$代表点集，$E$为边集。
需要注意的是，图的顶点集合不能为空，但边的集合可以为空。
我们常用$n$来代表顶点的数量,$m$代表边的数量。

图的分类

按点边数量分

根据点和边的数量来分可以分为:

• 稀疏图
• 稠密图
• 零图
  一般$m < nlogn$我们就认为这个图是稀疏图，否则是稠密图。简单来说就是 边少点多 即为稀疏图，反之则为稠密图。零图就是这张图的边集为空，即只有顶点的图。

边的分类

边分为:

• 无向边
• 有向边
  顾名思义，有向边就是带有方向的边，无向边就是不带有方向的边。

无向边相当于两条在相同的两个节点之间，方向不同的边。也就是a -> b & b -> a。

按边有无向分

首先边有向的就是 有向图，无向即为无向图。

• 有向图
• 无向图
  
  

其中如果无向图任意一对顶点之间都有边连接，也就是有$
\frac{n \cdot (n - 1)}{2}
$
条不重复的边,称为完全图,类似的，有向图任意一对顶点$[u,v]$之间都有两条有向边$(u,v),(v,u)$连接,称为有向完全图。

度

无向图的度

在无向图中,顶点的度是指某个顶点连出的边数。
例如下图，顶点4的度数为3,顶点1的度数为2。
在代码中度数一般用数组$d[i]$表示，表示顶点$i$的度数。

有向图的度

在有向图中，度分为两种:

• 入度
• 出度
  入度是指以该顶点为终点的有向边的数量,
  出度是指以该顶点为起点的有向边的数量。
  例如下图,顶点$4$的出度数量为$1$,入度为$2$。
  

度的性质

在有向图和无向图中，顶点的度数为边数的两倍。
在有向图中，入度数=出度数

图的存储

邻接矩阵

邻接矩阵是一种图的存储结构，它通过使用一维数组来表示每个顶点，并将边的信息存储在二维数组中，以矩阵的形式展现图中各顶点之间的邻接关系。简而言之，邻接矩阵以一种紧凑而清晰的方式描述了图的结构，其中每个顶点通过矩阵中的行和列相互关联。
对于有$n$个顶点的图 $G=(V,E)$ 来说，我们可以用一个 $n×n$ 的$01$矩阵 $g$ 来表示 $G$ 中各顶点的相邻关系。而$g_{ij} = 1$的时候代表$v_i$有一条连向$v_j$的边,0则没有。

这张无向图对应的01矩阵为:

0101
1011
0101
1110

这张有向图对应的01矩阵为:

0101
0001
0100
0010

仔细对比下即可领略。邻接矩阵在代码的体现就是一个二维数组$g[i][j]$。

邻接表

邻接表的思想是，对于图中的每一个顶点，用一个数组来记录这个点和哪些点相连。由于相邻的点会动态的添加，所以对于每个点，我们需要用vector(或者其他方式，例如前向星等)来记录，本文采用vector方式。
对于上面那张有向图，书写成邻接表的形式即为：

• h
• 1 2 4
• 2 4
• 3 2
• 4 3
  $h$即为顶点，后面跟着的是对应顶点通过有向边能到达的点。这个结构也是二维的，不过没有记录过多的信息，所以我们可以用变长数组vector来实现,vector<T> h[N];要想让1到2有一条边，直接h[1].push_back(2)即可。

使用技巧

一般在点数在5000以内，我们选择使用邻接矩阵，否则使用邻接表。